College of Liberal Arts & Sciences
6A40.11 - Apparent Depth - Pencil in the Block
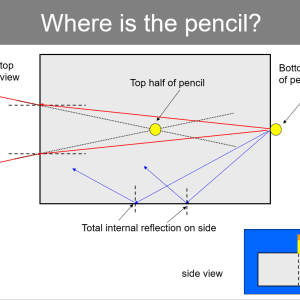
The 'Pencil in the Block' illusion works for 2 reasons:
- The index of refraction of the plastic block makes the lower part of the pencil that is attached to the back of the block appear to be in the same place as the top part of the pencil that is glued to the top of the block.
- The block is also designed so that when looking in the end you are able to see through the block to the pencil in the back. If you look in any other side of the block, the block acts as a mirror and you don't see the pencil. This is because all the sides are outside the critical angle.
There are two simple experiments that can be done to show apparent depth. The best is to place a transparent ruler on the overhead and then place a Plexiglass block on top of that. Focus the projector so that the ruler is in clear focus. Take another transparent ruler and raise it on the outside of the block until it is also in focus. The distance from the ruler under the block to the top of the block = d. The height that you have to raise the ruler on the outside of the block = h. Plugging these numbers into the formula d/d-h will give the approximate index of refraction of the block. A glass of water may be substituted for the block. Another version of this is to put a quarter into the bottom of a cup and fill the cup with water. Take another quarter and raise it on the outside of the cup until the two images look identical. Measure that height and plug the values into the above formula to get the approximate index of refraction.
- John F. Goehl Jr., "Previous Apparent-Depth Papers", TPT, Vol. 41, #1, Jan. 2003, p. 4.
- Adolf Cortel, "Apparent-Depth Demonstration Using a Plastic Box and Pins", TPT, Vol. 40, #7, Oct. 2002, p. 441.
- John F. Goehl Jr., "Is the Extrapolation Linear?", TPT, Vol. 26, #2, Feb. 1988, p. 105.
- Roger Blickensderfer, "Systematic Errors and Graphical Extrapolation", TPT, Vol. 23, #9, Dec. 1985, p. 545.
- James E. Kettler, "Some Optical Effects Using a Hollow Sphere and an Aquarium", TPT, Vol. 22, #3, Mar. 1984, p. 171
- John F. Goehl Jr., "Investigation of the Variation of Apparent Depth with Viewing Angle by Ray Tracing", AJP, Vol. 45, #10, Oct. 1977, p. 999.
- G. D. Freier and F. J. Anderson, "Oe-1", A Demonstration Handbook for Physics.
- G. D. Freier and F. J. Anderson, "Od-4", A Demonstration Handbook for Physics.
- Tik Liem, "Why Do We See Two Coins?", Investigation to Science Inquiry, p. 283.
- Tik Liem, "The Broken Pencil", Investigation to Science Inquiry, p. 281.
- Tik Liem, "The Invisible Penny,",Investigation to Science Inquiry, p. 278.
- Julius Sumner Miller, Q21 & A21, Millergrams I – Some Enchanting Questions for Enquiring Minds, p. 25 & 84.
Disclaimer: These demonstrations are provided only for illustrative use by persons affiliated with The University of Iowa and only under the direction of a trained instructor or physicist. The University of Iowa is not responsible for demonstrations performed by those using their own equipment or who choose to use this reference material for their own purpose. The demonstrations included here are within the public domain and can be found in materials contained in libraries, bookstores, and through electronic sources. Performing all or any portion of any of these demonstrations, with or without revisions not depicted here entails inherent risks. These risks include, without limitation, bodily injury (and possibly death), including risks to health that may be temporary or permanent and that may exacerbate a pre-existing medical condition; and property loss or damage. Anyone performing any part of these demonstrations, even with revisions, knowingly and voluntarily assumes all risks associated with them.